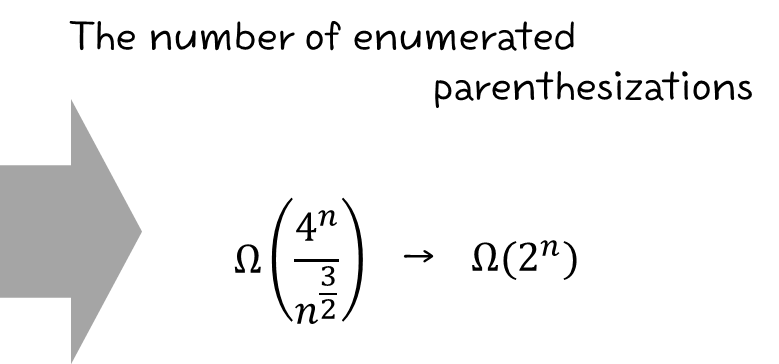이번에는 Greedy Algorithm을 살펴보도록 하겠다.
앞서 살펴본 Dynamic Programming의 경우에는 모든 경우의 수를 고려하여 최적의 솔루션을 찾는 방식이었다면
Greedy Algorithm은 어떤 순간에 최선으로 보이는 것을 선택해서 문제를 푸는 방식이다.
뭔 말이냐고!? 일단 하나 살펴보자.
[Overview]
어떤 활동(activity)들의 집합이 있다고 해보자.

이처럼 여러 activities들이 있을 때,
서로 겹치지 않고 동시에 할 수 있는 activities 중 가장 큰 subset을 선택하는 문제는 어떻게 풀면 좋을까?
예를 들자면,
강의실이 하나만 있을 때 여러 수업들을 어떻게 배치해야 가장 많은 수업들을 배치할 수 있는지를 정하는 것과 같다.
[Sample]
예시를 하나 들어보자.

위와 같이 activity들이 있다고 했을 때 어떤 조합들이 가능할까?!

우선 {a3, a9, a11} 집합의 경우 mutually compatible 하게 잘 묶여 있다.
서로 배타적이면서 같이 어울릴 수 있는 조합이라는 말이다.
하지만, 이 집합은 주어진 상황에서 largest set이라고 할 수는 없다.
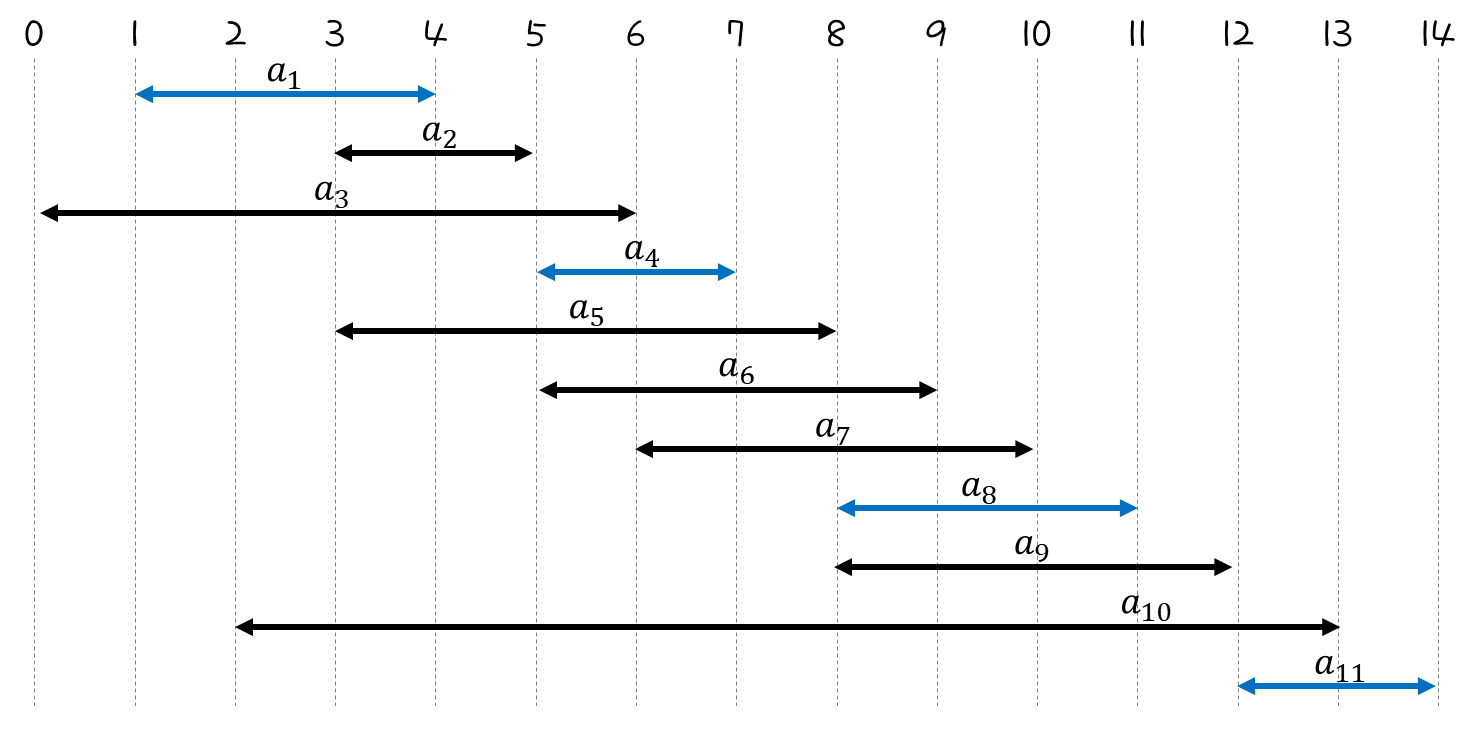
{a1, a4, a8, a11} set은 largest set이라고 할 수 있다.
4개보다 더 큰 조합은 찾을 수 없기 때문이다.
하지만 unique한 largest set은 아니다.

{a2, a4, a9, a11}의 경우도 largest set이다.
그런데, 이렇게 눈으로 정답을 찾는 것은 뭔가 좀..... ^^
[Optimal substructure]
일단 아래와 같은 문제가 주어졌다고 했을 때, 각 activity들의 시작 위치와 종료 위치를 작성해보자.

여기에서는 문제가 index 순서에 따라 종료 시간(f)이 순서대로 나와 있어서 정렬을 할 필요가 없지만,
종료 시간의 오름차순으로 정렬까지 해줘야 한다.

이렇게만 했으면 나머지는 쉽다.

제일 먼저 종료되는 시간 이후로 첫번째로 시작하는 activity를 선택하고,
그 activity가 종료되는 시간을 확인하고 또 다시, 그 종료 시간 이후로 시작하는 activity를 찾고... 반복하면 된다.
끝이다.
뭔가 허무한데, 끝이다.
[Elements of the greedy strategy]
어째서 Dynamic Programming과 다르게 Greedy Algorithm은 이렇게 문제를 풀 수 있는지에 대해서 알아보자.

subproblem을 모두 풀어야지만 솔루션을 선택할 수 있는 경우에는 Dynamic Programming 문제이고,
모든 subproblem을 풀기 전에 솔루션을 선택할 수 있는 문제는 Greedy Algorithm을 적용할 수 있다.

Zero-One 배낭 문제는 물건을 갯수 단위로만 가방안에 넣을 수 있는 경우에 해당하는 문제이다.
물건들의 가격과 무게가 모두 다르다고 했을 때, 어떻게 넣어야지 가장 비싸게 물건을 훔칠 수 있는지를 찾는 것이다.
모든 조합을 고려해야 문제가 풀리는 것이다.

이와는 다르게, 만약 아이템을 조각내서 가방에 담을 수 있다고 하면 어떻게 될까?
그러면 개별 단가가 가장 비싼 것들로 정렬해서 그냥 그렇게 넣으면 된다.
담을 수 있는 무게와 딱 떨어지지 않을 경우에는 조각내면 된다.
모든 조합을 고려할 필요가 없는 것이다.
예시를 들어보자.
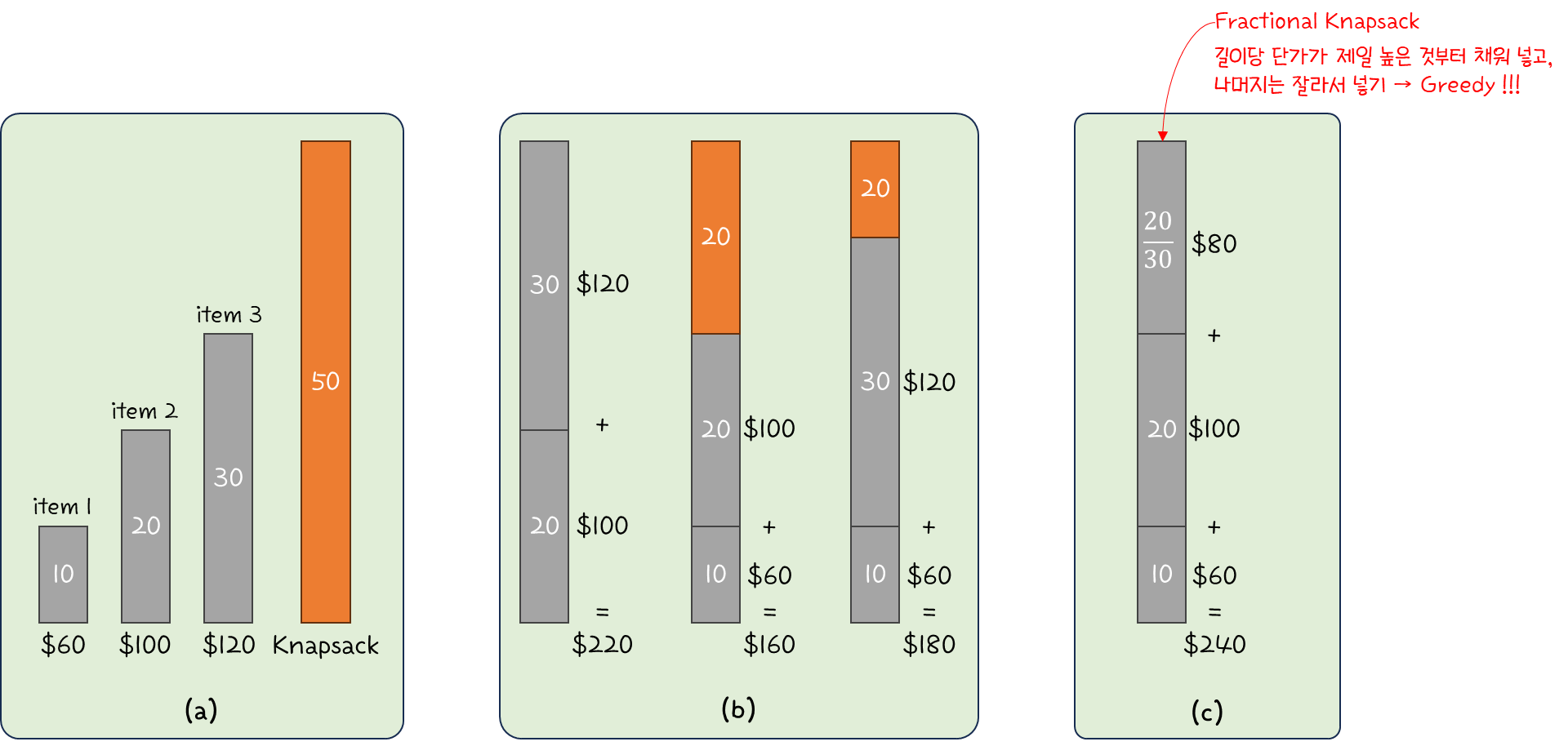
⒜와 같이 상황이 주어졌다고 해보자.
배낭은 담을 수 있는 무게의 한계가 있다.
⒝는 Dynamic Programming 방식으로 해답을 찾아보는 것이다. 모든 조합을 검토하는 것이다.
⒞는 Greedy Algorithm 방식이다. 무게당 단가를 계산해서 가장 비싼 것들부터 넣기 시작하다가
무게 제한에 걸리는 시점에는 해당 아이템을 잘라내서 무게에 맞추면 되는 것이다.
확실히 문제의 유형이 다르다!!!
'Programming > Algorithm' 카테고리의 다른 글
| 알고리즘 #2 - Dynamic Programming #4 - Matrix-Chain Multiplication #1 (0) | 2024.04.07 |
|---|---|
| 알고리즘 #2 - Dynamic Programming #3 - Longest-Common-Subsequence #1 (0) | 2024.03.25 |
| 알고리즘 #2 - Dynamic Programming #2 - Rod-Cutting #1 (0) | 2024.03.09 |
| 알고리즘 #2 - Dynamic Programming #1 - Assembly-line scheduling #1 (0) | 2024.02.28 |
| 알고리즘 #1 - 정렬 문제 #8 - Radix Sort #1 (1) | 2024.02.21 |